Два треугольника называются подобными, если отношения всех их соответствующих сторон равны. Отношение \(k\) соответствующих сторон подобных треугольников называется коэффициентом подобия этих треугольников.

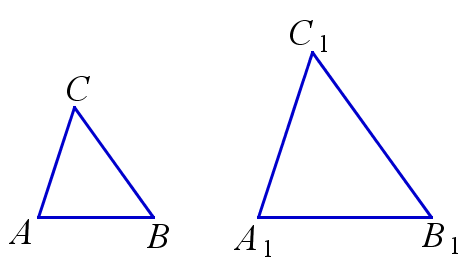
$$ \triangle{ABC} \backsim \triangle{A_1B_1C_1} \Leftrightarrow \frac{AB}{A_1B_1}=\frac{AC}{A_1C_1}=\frac{BC}{B_1C_1}; $$ $$ k=\frac{AB}{A_1B_1}=\frac{AC}{A_1C_1}=\frac{BC}{B_1C_1} $$

Если треугольники подобны, то все их соответствующие углы равны.

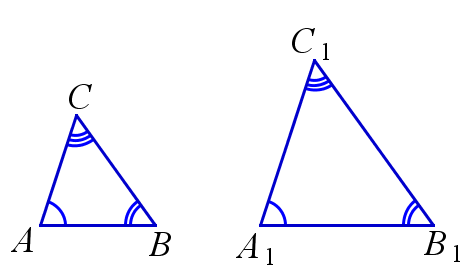
$$\triangle{ABC} \backsim \triangle{A_1B_1C_1} \Rightarrow \angle{A}=\angle{A_1}, \, \angle{B}=\angle{B_1}, \, \angle{C}=\angle{C_1}$$

Если отношения двух сторон треугольников и равны углы между этими сторонами, то такие треугольники подобны.

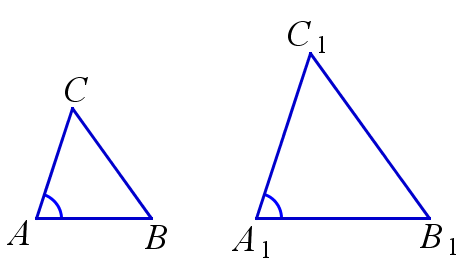
$$ \frac{AB}{A_1B_1}=\frac{AC}{A_1C_1}, \, \angle{A}=\angle{A_1} \Rightarrow \triangle{ABC} \backsim \triangle{A_1B_1C_1} $$

Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.

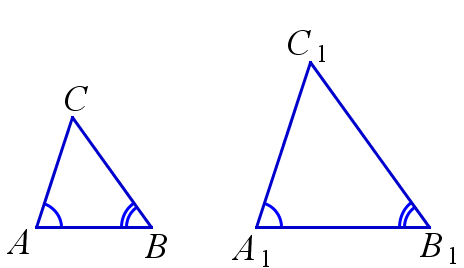
$$ \angle{A}=\angle{A_1}, \, \angle{B}=\angle{B_1} \Rightarrow \triangle{ABC} \backsim \triangle{A_1B_1C_1} $$

Если отношения всех соответствующих сторон треугольников равны, то такие треугольники подобны.

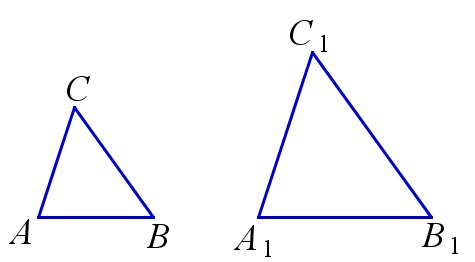
$$ \frac{AB}{A_1B_1}=\frac{AC}{A_1C_1}=\frac{BC}{B_1C_1} \Rightarrow \triangle{ABC} \backsim \triangle{A_1B_1C_1} $$

Отношение любых двух соответствующих линейных элементов подобных треугольников равно коэффициенту подобия этих треугольников. (Соответствующие линейные элементы – это отрезки подобных фигур, полученные одинаковой конструкцией. Например, медианы треугольников, проведённые к соотвествующим сторонам, радиусы описанных окружностей, периметры, и так далее.)

$$ \frac{AB}{A_1B_1}=\frac{AC}{A_1C_1}=\frac{BC}{B_1C_1} \Rightarrow \triangle{ABC} \backsim \triangle{A_1B_1C_1} $$

Отношение площадей подобных треугольников равно квадрату коэффициента подобия.

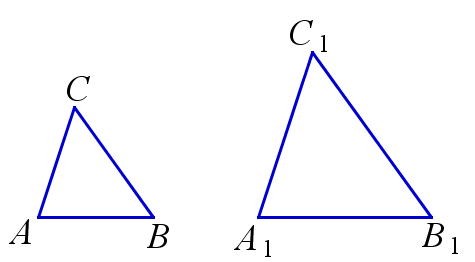
$$ \frac{AB}{A_1B_1}=\frac{AC}{A_1C_1}=\frac{BC}{B_1C_1}=k \, \Rightarrow \, \frac{S_{ABC}}{S_{A_1B_1C_1}}=k^2 $$

Если стороны двух треугольников лежат на соответственно параллельных или совпадающих прямых, то такие треугольники подобны. В частности, параллельные прямые отсекают от угла, либо вертикальных углов, подобные треугольники.

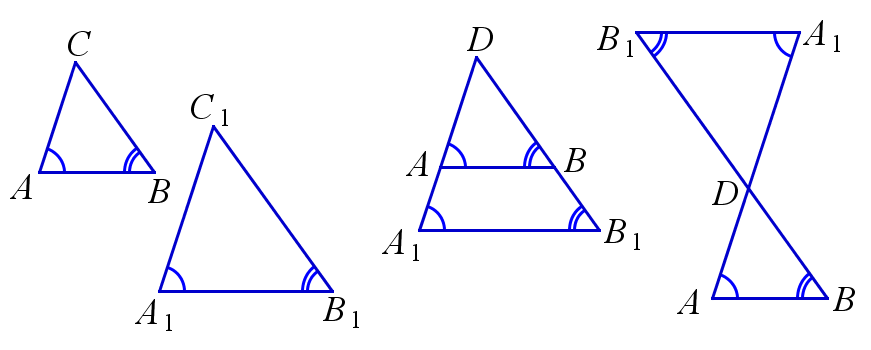
$$ AB || A_1B1, \, AC || A_1C_1, \, BC ||B_1C_1 \Rightarrow \triangle{ABC} \backsim \triangle{A_1B_1C_1}; $$ $$ AB || A_1B_1, \, D=AA_1 \cap BB_1 \Rightarrow \triangle{ABD} \backsim \triangle{A_1B_1D} $$

При пересечении диагоналей трапеции, а также продолжений её боковых сторон, образуются подобные треугольники, прилежащие к основаниям трапеции. Коэффициент подобия в обоих случаях равен отношению оснований трапеции.

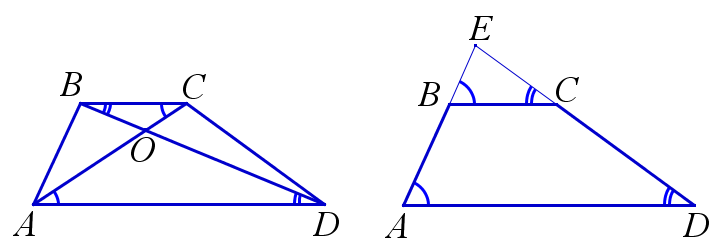
$$ \triangle{AOD} \backsim \triangle{COB}, \quad k=\frac{AD}{BC}; $$ $$ \triangle{AED} \backsim \triangle{BEC}, \quad k=\frac{AD}{BC} $$

При пересечении двух прямых с окружностью образуются подобные треугольники.

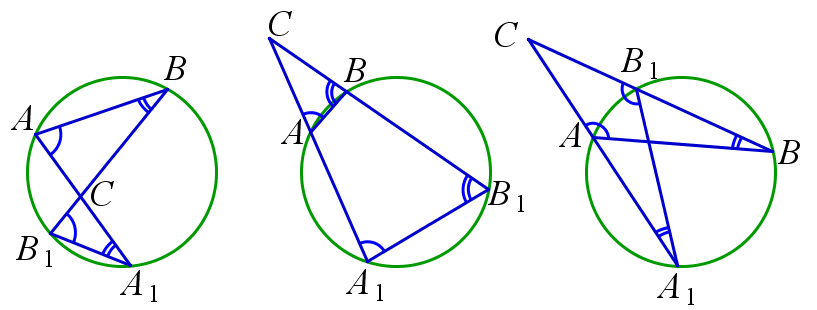
$$ \triangle{ABC} \backsim \triangle{B_1A_1C}, \quad k=\frac{AB}{B_1A_1}=\frac{AC}{B_1C}\frac{BC}{A_1C} $$

Пусть к окружности проведена кастельная \(CB\) и секущая \(CA\), пересекающая окружность во второй раз в точке \(A_1\). Тогда \(\triangle{ABC} \backsim \triangle{BA_1C}\).

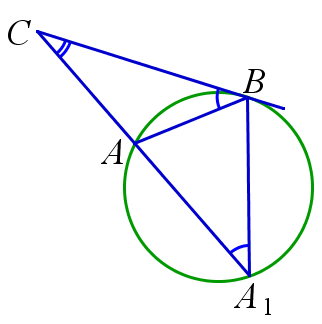
$$ \triangle{ABC} \backsim \triangle{BCA_1}, \quad k=\frac{AB}{BA_1}=\frac{AC}{BC}\frac{BC}{A_1C} $$