Треугольник называется прямоугольным, если один из его углов прямой. Стороны, прилежащие к прямому углу, называются катетами прямоугольного треугольника, а сторона, противолежащая прямому углу – гипотенузой прямоугольного треугольника.

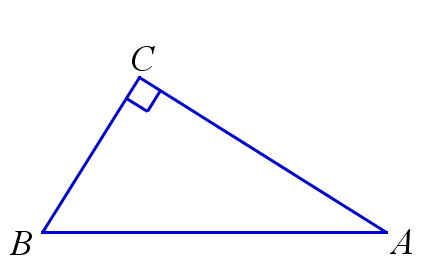
\(\triangle{ABC}\) прямоугольный;

\(AC\), \(BC\) – катеты, \(AB\) – гипотенуза

Медиана прямоугольного треугольника, проведённая к гипотенузе, равна половине гипотенузы.

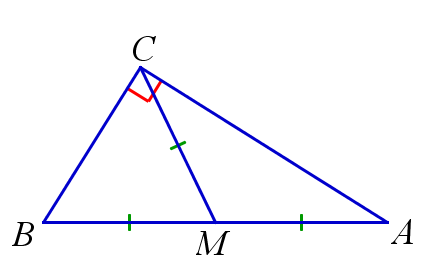
\(\angle{C}=90^{\circ}, \, CM\) – медиана \(\triangle{ABC} \, \Rightarrow \, AM=BM=CM \)

Если в треугольнике медиана равна половине стороны, к которой она проведена, то этот треугольник прямоугольный.

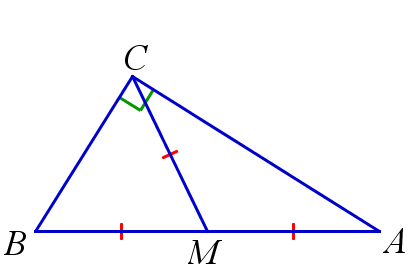
\(CM\) – медиана \( \triangle{ABC}, \, AM=BM=CM \, \Rightarrow \, \angle{C}=90^{\circ}\)

1. В прямоугольном треугольнике катет, лежащий напротив угла в \(30^{\circ}\), равен половине гипотенузы.

2. Если в прямоугольном треугольнике катет равен половине гипотенузы, то угол, противолежащий этому катету, равен \(30^{\circ}\).

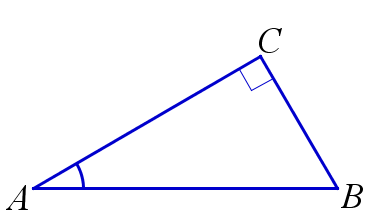
$$ \angle{A}=30^{\circ} \Leftrightarrow BC=\frac{1}{2}AB $$

1. По двум катетам: если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то данные треугольники равны.

2. По гипотенузе и катету: если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого прямоугольного треугольника, то данные треугольники равны.

3. По гипотенузе и острому углу: если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то данные треугольники равны.

4. По катету и острому углу: если катет и острый угол одного прямоугольного треугольника соответственно равны катету и острому углу другого прямоугольного треугольника, то данные треугольники равны.

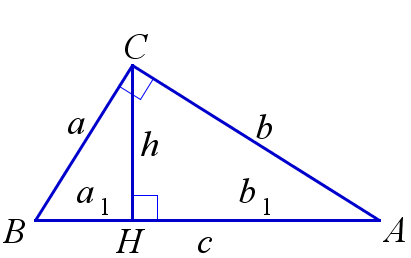
Пусть в треугольнике \(ABC\) \(\angle{C}=90^{\circ}\), \(a=BC\), \(b=AC\) – катеты, \(c=AB\) – гипотенуза, \(h=CH\) – высота к гипотенузе, \(a_1=BH\), \(b_1=AH\) – проекции катетов на гипотенузу. Тогда

\( \quad 1. \quad a_1b_1=h^2; \)

\( \quad 2. \quad a_1c=a^2; \)

\( \quad 3. \quad b_1c=b^2; \)

\( \quad 4. \quad a_1+b_1=c. \)

В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.

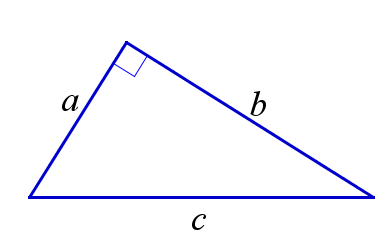
$$ a^2+b^2=c^2 $$

Если в треугольнике сумма квадратов двух сторон равна квадрату третьей стороны, то этот треугольник прямоугольный.

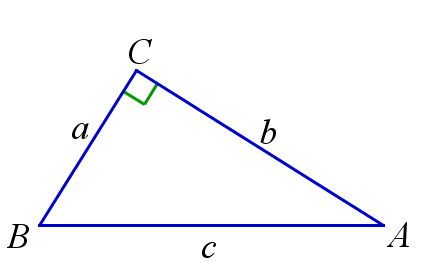
$$ a^2+b^2=c^2 \Rightarrow \angle{C}=90^{\circ} $$

Высота, проведённая к гипотенузе, делит прямоугольный треугольник на два треугольника подобных друг другу и исходному треугольнику.

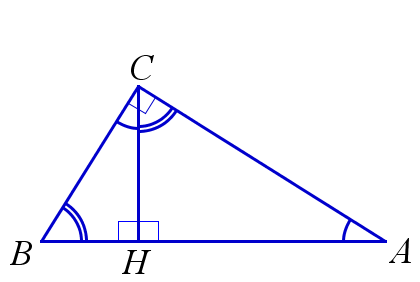
$$ \triangle{ACH} \backsim \triangle{CBH} \backsim \triangle{ABC} $$

Центром окружности, описанной около прямоугольного треугольника, является середина гипотенузы. Радиус описанной окружности прямоугольного треугольника равен половине гипотенузы.

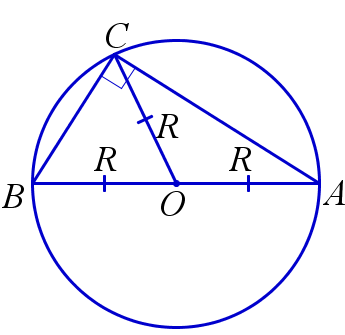
$$ R=\frac{1}{2}AB $$

Радиус \(r\) окружности, вписанной в прямоугольный треугольник, может быть вычислен по формуле

$$ r=\frac{a+b-c}{2}, $$

где \(a\) и \(b\) – катеты треугольника, \(c\) – его гипотенуза.

Тригонометрические функции углов прямоугольного треугольника

Смотрите следующий раздел.