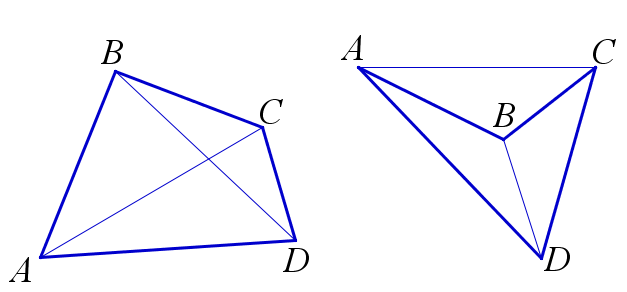
Четырёхугольником называется фигура, состоящая из четырёх точек \(A\), \(B\), \(C\), \(D\), никакие три из которых не лежат на одной прямой, и четырёх последовательно соединяющих их отрезков \(AB\), \(BC\), \(CD\), \(DA\), никакие два из которых не имеют общих внутренних точек. Данный четырёхугольник обозначается \(ABCD\), и точки \(A\), \(B\), \(C\), \(D\) называются его вершинами, а отрезки \(AB\), \(BC\), \(CD\), \(DA\) – его сторонами. Вершины, являющиеся концами одной стороны четырёхугольника, называются смежными, а вершины, не принадлежщие одной стороне четырёхугольника – противоположными. Стороны, имеющие общую вершину, называются смежными сторонами, а не имеющие общих вершин – противоположными сторонами четырёхугольника. Отрезки \(AC\) и \(BD\), соединяющие противоположные вершины четырёхугольника, называются диагоналями четырёхугольника.

Четырёхугольник называется выпуклым, если он лежит по одну сторону от любой прямой, проходящей через любые две его смежные вершины. В противном случае четырёхугольник называется невыпуклым. Диагонали выпуклого четырёхугольника лежат внути него и пересекаются. Одна из диагоалей невыпуклого четырёхугольника лежит снаружи, а другая внутри него, и эти диагонели не пересекаются.

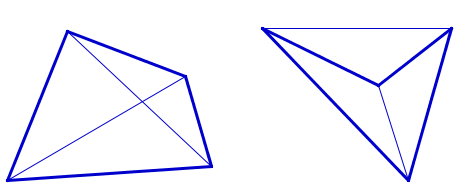
выпуклый (слева) и невыпуклый (справа) четырёхугольники

Углы \(DAB\), \(ABC\), \(BCD\) и \(CDA\) называются внутренними углами четырёхугольника \(ABCD\) (в случае невыпуклого четырёхугольника один из них больше \(180^{\circ}\)).

Сумма внутренних углов четырёхугольника равна \(360^{\circ}\).

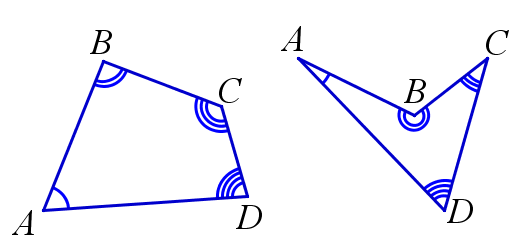
$$ \angle{DAB}+\angle{ABC}+\angle{BCD}+\angle{CDA}=360^{\circ} $$