Четырёхугольник называется параллелограммом, если его противоположные стороны попарно параллельны.

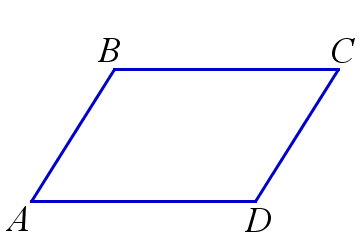
\(ABCD\) – параллелограмм \(\, \Leftrightarrow \, AB||CD\) и \(BC||AD\)

1. Противоположные стороны параллелограмма равны.
2. Противоположные углы параллелограмма равны.
3. Сумма смежных углов параллелограмма равна \(180^{\circ}\).
4. Диагонали параллелограмма делятся точкой пересечения пополам.

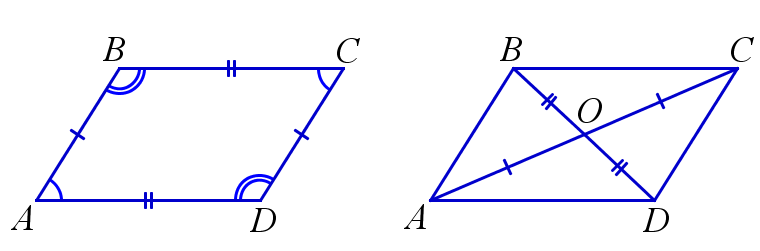
\(ABCD\) – параллелограмм \(\Rightarrow\) \( AB=CD, \, BC=AD; \)
\(ABCD\) – параллелограмм \(\Rightarrow\) \(\angle{A}=\angle{C}, \, \angle{B}=\angle{D}; \)
\(ABCD\) – параллелограмм \(\Rightarrow\) \(\angle{A}+\angle{B}=180^{\circ}, \, \angle{A}+\angle{D}=180^{\circ}, \, \angle{C}+\angle{B}=180^{\circ}, \, \angle{C}+\angle{D}=180^{\circ};\)
\(ABCD\) – параллелограмм, \(AC \cap BD =O\) \(\Rightarrow\) \(AO=CO, \, BO=DO \)

1. Если в четырёхугольнике противоположные стороны попарно равны, то этот четырёхугольник – параллелограмм.
2. Если в четырёхугольнике противоположные углы попарно равны, то этот четырёхугольник – параллелограмм.
3. Если в четырёхугольнике две противоположные стороны параллельны и равны, то этот четырёхугольник – параллелограмм.
4. Если в четырёхугольнике диагонали точкой пересечения делятся пополам, то этот четырёхугольник – параллелограмм.

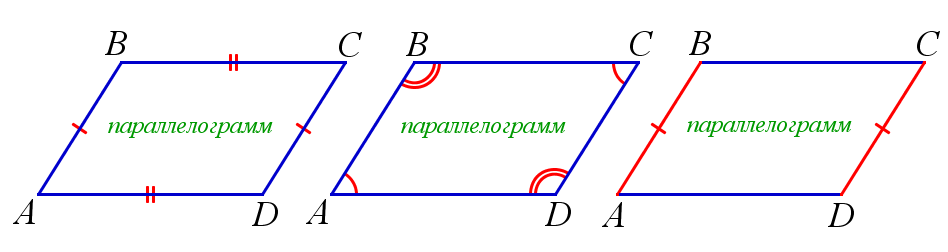
\( AB=CD, \, BC=AD \) \(\Rightarrow\) \(ABCD\) – параллелограмм\(;\)
\(\angle{A}=\angle{C}, \, \angle{B}=\angle{D} \) \(\Rightarrow\) \(ABCD\) – параллелограмм\(;\)
\( AB=CD, \, AB||CD \) \(\Rightarrow\) \(ABCD\) – параллелограмм\(;\)

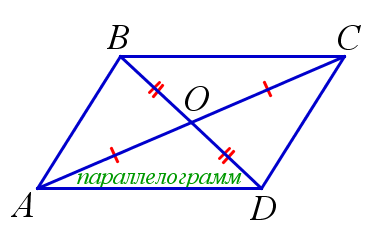
\( AO=CO, \, BO=DO \) \(\Rightarrow\) \(ABCD\) – параллелограмм

Ромб, прямоугольник и квадрат являются параллелограммами. Остальные параллелограммы называют параллелограммами общего вида

Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.

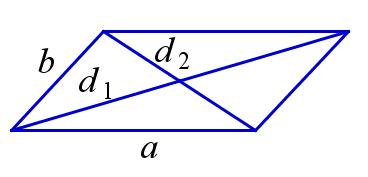
\( d_1^2+d_2^2=2a^2+2b^2 \)

1. Площадь параллелограмма равна произведению его стороны на высоту, проведённую к этой стороне.

\( S=ah \)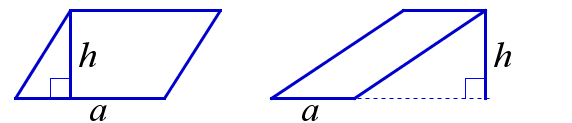

2. Площадь параллелограмма равна произведению его смежных сторон на синус угла между ними.

\( S=ab\sin{\gamma} \)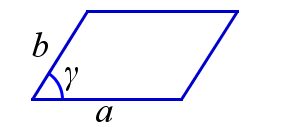

3. Площадь параллелограмма равна половине произведения его диагоналей на синус угла между ними.

\( S=\frac{1}{2}d_1d_2\sin{\varphi} \)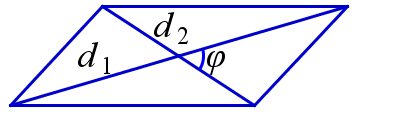