Трапеция
❒ Определение трапеции
❒ Свойства трапеции
❒ Средняя линия трапеции
❒ Определение равнобедренной трапеции
❒ Свойства равнобедренной трапеции
❒ Признаки равнобедренной трапеции
❒ Свойство середин оснований трапеции
❒ Площадь трапеции
Определение трапеции
Трапецией называется четырёхугольник, две стороны которого параллельны, а две другие не параллельны. Параллельные стороны трапеции называются её основаниями, а непараллельные – боковыми сторонами трапеции.
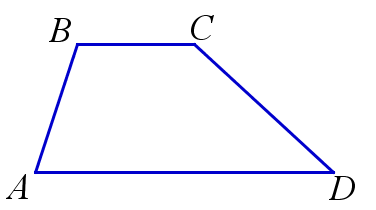
\(ABCD\) – трапеция;
\(AD, \, BC\) – основания, \(AB, \, CD\) – боковые стороны трапеции \(ABCD\)
Свойства трапеции
1. Сумма углов, прилежащих к боковой стороне трапеции, равна \(180^{\circ}\).
2. Каждая диагональ трапеции образует с её основаниями равные углы.
3. При пересечении диагоналей трапеции и продолжений её боковых сторон образуются подобные треугольники, прилежащие к основаниям.
4. Биссектрисы смежных углов трапеции перпендикулярны.
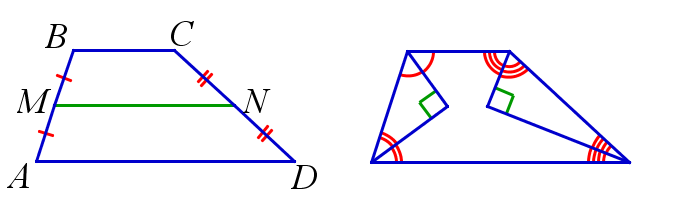
\(ABCD\) – трапеция \(\Rightarrow \, \angle{DAB}+\angle{ABC}=180^{\circ}, \, \angle{ADC}+\angle{DCB}=180^{\circ};\)
\(ABCD\) – трапеция \(\Rightarrow \, \angle{CAD}=\angle{ACB}, \, \angle{BDA}=\angle{DBC};\)
\(ABCD\) – трапеция, \(AC \cap BD=O\) \(\Rightarrow \, \triangle{AOD} \backsim \triangle{COB};\)
\(ABCD\) – трапеция, \(AB \cap CD=E\) \(\Rightarrow \, \triangle{AED} \backsim \triangle{BEC}\)
Средняя линия трапеции
Определение. Средней линией трапеции называется отрезок, соединяющий середины боковых сторон трапеции.
Теорема о средней линии трапеции. Средняя линия трапеции параллельна основаниям трапеции и равна их полусумме.
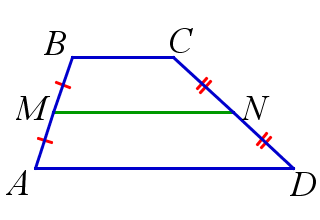
\( AD||BC, \, M\) – середина \(AB, \, N\) – середина \(CD \, \Rightarrow \) $$ MN||AD, \, MN||BC, \, MN=\frac{1}{2}(AD+BC)$$
Определение равнобедренной трапеции
Трапеция называется равнобедренной, если её боковые стороны равны.
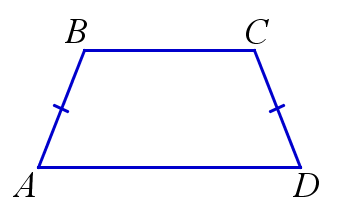
\(ABCD\) – равнобедренная трапеция
Свойства равнобедренной трапеции
1. В равнобедренной трапеции углы при каждом основании равны.
2. Диагонали равнобедренной трапеции равны.
3. Ранобедренную трапецию можно вписать в окружность.
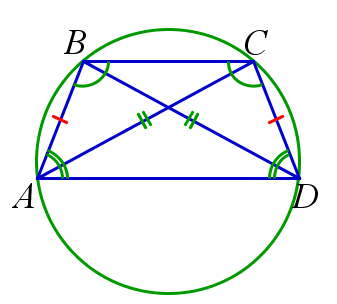
\(ABCD\) трапеция,\( \, AB=CD \, \Rightarrow \, \angle{ABC}=\angle{DCB}, \, \angle{BAD}=\angle{CDA}; \)
\(ABCD\) трапеция,\( \, AB=CD \, \Rightarrow \, AC=BD; \)
\(ABCD\) трапеция,\( \, AB=CD \, \Rightarrow \, ABCD\) вписанная
Признаки равнобедренной трапеции
1. Если углы при некотором основании трапеции равны, то эта трапеция равнобедренная.
2. Если диагонали трапеции равны, то эта трапеция равнобедренная.
3. Если трапецию можно вписать в окружность, то эта трапеция равнобедренная.
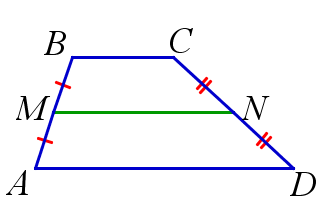
\( AD||BC, \, M\) – середина \(AB, \, N\) – середина \(CD \, \Rightarrow \) $$ MN||AD, \, MN||BC, \, MN=\frac{1}{2}(AD+BC)$$
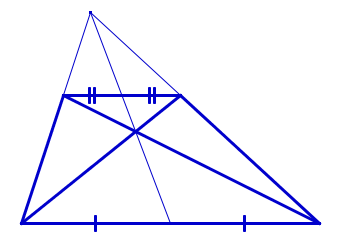
Свойство середин оснований трапеции
Середины оснований трапеции, точка пересечения её диагоналей и точка пересечения продолжений боковых сторон лежат на одной прямой.
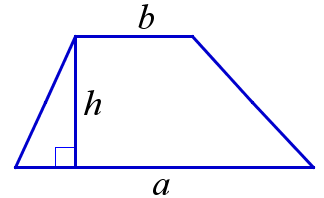
Площадь трапеции
1. Площадь трапеции равна половине произведения суммы её оснований на высоту трапеции.
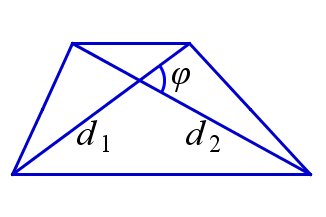
2. Площадь трапеции равна половине произведения её диагоналей на синус угла между ними.
 |  |
|
$$ S=\frac{1}{2}(a+b)h$$ | $$ S=\frac{1}{2} d_1d_2\sin{\varphi}$$ |