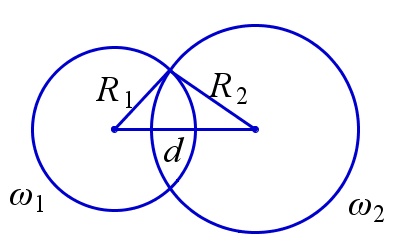
Пересекающиеся окружности

Говорят, что две окружности пересекаются, если они имеют две общие точки.

Пусть $R_1$ и $R_2$ – радиусы окружностей $\omega_1$ и $\omega_2$ и $d$ – расстояние между их центрами. Окружности $\omega_1$ и $\omega_2$ пересекаются тогда и только тогда, когда числа $R_1$, $R_2$, $d $ являются длинами сторон некоторого треугольника, т. е. удовлетворяют всем неравенствам треугольника: $$ R_1+R_2 > d, \, R_1+d > R_2, \, R_2+d > R_1. $$