Основные свойства площади
Понятие площади
Площадь – это функция, которая сопоставляет фигурам на плоскости неотрицательные действительные числа так, что выполнены следующие условия (аксиомы площади).
1. Площадь квадрата со стороной 1 равна 1.
2. Если фигура \(\Phi\) разбита на несколько частей \(\Phi_1, \Phi_2, \ldots , \Phi_n,\) никакие две из которых не имеют общих внутренних точек, то площадь фигуры \(\Phi\) равна сумме площадей фигур \(\Phi_1, \Phi_2, \ldots , \Phi_n\).
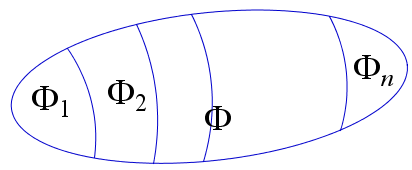
$$ S_{\Phi}=S_{\Phi_1}+S_{\Phi_2}+ \ldots +S_{\Phi_n} $$
3. Площади равных фигур равны.
Монотонность площади
Если фигура \(\Phi_2\) содержится в фигуре \(\Phi_1\), то площадь фигуры \(\Phi_2\) не превосходит площади фигуры \(\Phi_1\). При этом площадь \(\Phi_1\) равна сумме площади \(\Phi_2\) и площади фигуры \(\Phi_1 \setminus \Phi_2\), состоящей из всех точек \(\Phi_1\), которые не принадлежат \(\Phi_2\).
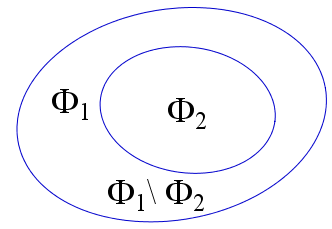
$$ S_{\Phi_2} \leq S_{\Phi_1} $$ $$ S_{\Phi_1} = S_{\Phi_2}+S_{\Phi_1 \setminus \Phi_2} $$
Площади подобных фигур
Отношение площадей подобных фигур равно квадрату коэффициента подобия.
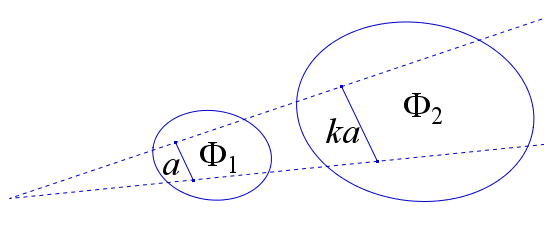
$$ S_{\Phi_2}=k^2S_{\Phi_1} $$