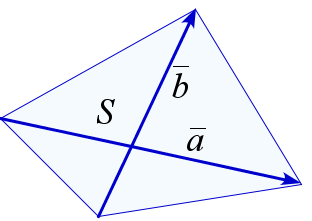
Площадь четырёхугольника через скалярное произведение

Пусть векторы \(\overline{a}=(x_1,\, y_1)\),   \(\overline{b}=(x_2,\, y_2)\) направлены вдоль диагоналей четырёхугольника (координаты векторов – в ортонормированном базисе). Тогда площадь \(S\) этого четырёхугольника может быть вычислена по формулам: $$ S=\frac{1}{2}\sqrt{\overline{a}^{\,2}\,\overline{b}^{\,2}-(\overline{a}\cdot\overline{b})^{2}}, \quad S=\frac{1}{2}|x_1y_2-x_2y_1|. $$