Проекция и скалярное произведение

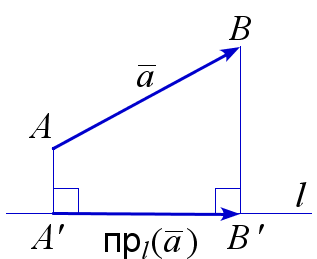
Проекцией вектора \(\overline{a}=\overrightarrow{AB}\) на ось \(l\) называется вектор \(пр_{l}(\overline{a})=\overrightarrow{A'B'}\), где \(A'\) и \(B'\) – основания перпендикуляров из точек \(A\) и \(B\) на прямую \(l\). Если \(l\) – прямая с направляющим вектором \(\overline{b}\) (т. е. \(\overrightarrow{MN}=\overline{b}\) для некоторых точек \(M\) и \(N\) прямой \(l\)), то \(\overline{a}\cdot\overline{b}=пр_{l}(\overline{a})\cdot\overline{b}\).

$$ \overrightarrow{A'B'}=пр_{l}\left(\overrightarrow{AB}\right) $$		\(\overline{a}\cdot\overline{b}=пр_{l}(\overline{a})\cdot\overline{b}\)