Скалярное произведение векторов
❒ Угол между векторами
❒ Определение скалярного произведения
❒ Косинус угла между векторами
❒ Проекция и скалярное произведение
❒ Свойства проекции вектора на ось
❒ Свойства скалярного произведения
❒ Ортогональные векторы
❒ Ортонормированный базис
❒ Координаты вектора в ортонормированном базисе
❒ Основные формулы в прямоугольных координатах
❒ Площадь параллелограмма через скалярное произведение
❒ Площадь треугольника через скалярное произведение
❒ Площадь четырёхугольника через скалярное произведение
Угол между векторами
Пусть \(\overline{a}\) и \(\overline{b}\) – два ненулевых вектора. Отложим их от одной точки \(O\) плоскости: пусть \(\overline{a}=\overrightarrow{OA}\), \(\overline{b}=\overrightarrow{OB}\). Углом между ненулевыми векторами \(\overline{a}=\overrightarrow{OA}\) и \(\overline{b}=\overrightarrow{OB}\) называется величина угла \(AOB\).
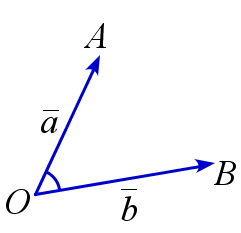
$$ \widehat{\overline{a},\overline{b}}=\angle{AOB} $$
Определение скалярного произведения
Салярным произведением двух ненулевых векторов \(\overline{a}\) и \(\overline{b}\) называется число \(\overline{a}\cdot\overline{b}\) равное произведению длин этих векторов на косинус угла между ними. Если хотя бы один из векторов \(\overline{a}\) и \(\overline{b}\) нулевой, то скалярное произведение \(\overline{a}\cdot\overline{b}\) по определению равно нулю.
$$ \overline{a}\cdot\overline{b}=|\overline{a}||\overline{b}|\cos\left(\,\widehat{\overline{a},\,\overline{b}}\,\right) $$
Косинус угла между векторами
Косинус угла между ненулевыми векторами может быть вычислен по формуле $$ \cos\left(\,\widehat{\overline{a},\,\overline{b}}\,\right)=\frac{\overline{a}\cdot\overline{b}}{|\overline{a}|\,|\overline{b}|}. $$

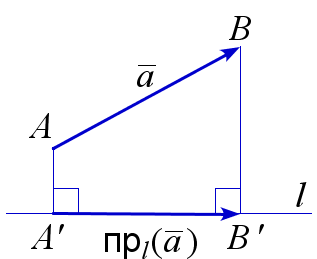
Проекция и скалярное произведение
Проекцией вектора \(\overline{a}=\overrightarrow{AB}\) на ось \(l\) называется вектор \(пр_{l}(\overline{a})=\overrightarrow{A'B'}\), где \(A'\) и \(B'\) – основания перпендикуляров из точек \(A\) и \(B\) на прямую \(l\). Если \(l\) – прямая с направляющим вектором \(\overline{b}\) (т. е. \(\overrightarrow{MN}=\overline{b}\) для некоторых точек \(M\) и \(N\) прямой \(l\)), то \(\overline{a}\cdot\overline{b}=пр_{l}(\overline{a})\cdot\overline{b}\).
 |
 |
|
|
$$ \overrightarrow{A'B'}=пр_{l}\left(\overrightarrow{AB}\right) $$ |
\(\overline{a}\cdot\overline{b}=пр_{l}(\overline{a})\cdot\overline{b}\) |
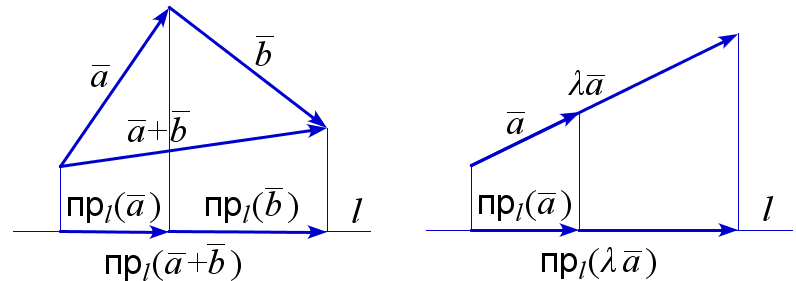
Свойства проекции вектора на ось
Для любых векторов \(\overline{a}\), \(\overline{b}\), любого числа \(\lambda\) и любой прямой \(l\):
1. \(пр_l(\overline{a}\pm\overline{b})=пр_l(\overline{a})\pm пр_l(\overline{b})\);
2. \(пр_l(\lambda\overline{a})=\lambda \, пр_l(\overline{a})\).
Свойства скалярного произведения
Для любых векторов \(\overline{a}\), \(\overline{b}\), \(\overline{c}\) и любого числа \(\lambda\):
1. \(\overline{a}\cdot \overline{b}=\overline{b}\cdot \overline{a}\);
2. \(\overline{a}\cdot (\overline{b}\pm\overline{c})=\overline{a}\cdot \overline{b}\pm\ \overline{a}\cdot\overline{c},\)
\((\overline{b}\pm\overline{c})\cdot\overline{a}=\overline{b}\cdot\overline{a}\pm\overline{c}\cdot\overline{a}\);
3. \((\lambda\overline{a})\cdot \overline{b}=\overline{a}\cdot (\lambda\overline{b})=\lambda\, (\overline{a}\cdot \overline{b})\);
4. \({\overline{a}}^{\, 2} \geq 0\), причём \({\overline{a}}^{\, 2}=0 \, \Leftrightarrow \, \overline{a}=\overline{0}\quad\)
(здесь \({\overline{a}}^{\, 2}=\overline{a}\cdot \overline{a}\));
5. \(\sqrt{\overline{a}^{2}}=|\overline{a}|\);
6. \(|\overline{a}\cdot\overline{b}|\leq|\overline{a}|\,|\overline{b}|\), причём
\(|\overline{a}\cdot\overline{b}|=|\overline{a}|\,|\overline{b}| \Leftrightarrow \overline{a}||\overline{b}\)
(неравенство Коши-Буняковского).
Ортогональные векторы
Векторы \(\overline{a}\) и \(\overline{b}\) называются ортогональными (обозначение: \(\overline{a}\perp\overline{b}\)), если их скалярное произведение равно нулю. Два вектора ортогональны тогда и только тогда, когда они перепендикулярны (т. е. угол между ними равен \(90^{\circ}\)) или хотя бы один из них нулевой.
Ортонормированный базис
Ортонормированным базисом векторов на плоскости называются пара ортогональных (перпендикулярных) векторов \(\overline{i}\), \(\overline{j}\) единичной длины. Таким образом, \(\overline{i}\), \(\overline{j}\) – ортонормированный базис тогда и только тогда, когда $$ \overline{i}\cdot\overline{j}=0, \quad |\overline{i}|=1, \quad |\overline{j}|=1. $$ Координаты векторов в ортонормированном базисе называют также прямоугольными координатами.
Координаты вектора в ортонормированном базисе
Если \(\overline{a}=(x,\,y)\) – координаты вектора \(\overline{a}\) в ортонормированном базисе \(\overline{i}\), \(\overline{j}\) то справедливы равенства:
1. \(\overline{a}=x\,\overline{i}+y\,\overline{j}\);
2. \(\overline{a}\cdot\overline{i}=x\), \(\overline{a}\cdot\overline{j}=y\);
3. \(пр_{OX}(\overline{a})=x\,\overline{i}\), \(пр_{OY}(\overline{a})=y\,\overline{j}\), где \(OX\) и \(OY\) – прямые с направляющими векторами \(\overline{i}\) и \(\overline{j}\) (оси координат).
Основные формулы в прямоугольных координатах
Пусть \(\overline{a}=(x_1,\, y_1)\), \(\overline{b}=(x_2,\, y_2)\) – координаты векторов \(\overline{a}\) и \(\overline{b}\) в одном и том же ортонормированном базисе. Тогда
1. \(\overline{a}\cdot\overline{b}=x_1x_2+y_1y_2\);
2. \(|\overline{a}|=\sqrt{x_1^2+y_1^2}\), \(|\overline{b}|=\sqrt{x_2^2+y_2^2}\);
3. \(\cos\left(\,\widehat{\overline{a},\overline{b}}\,\right)=\frac{x_1x_2+y_1y_2}{\sqrt{x_1^2+y_1^2}\sqrt{x_2^2+y_2^2}}\);
4. \(\sin\left(\,\widehat{\overline{a},\overline{b}}\,\right)=\frac{|x_1y_2-x_2y_1|}{\sqrt{x_1^2+y_1^2}\sqrt{x_2^2+y_2^2}}\).
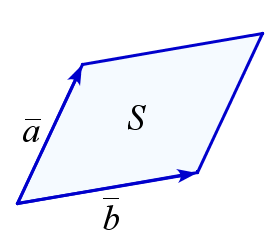
Площадь параллелограмма через скалярное произведение
Пусть векторы \(\overline{a}=(x_1,\, y_1)\), \(\overline{b}=(x_2,\, y_2)\) направлены вдоль смежных сторон параллелограмма (координаты векторов – в ортонормированном базисе). Тогда площадь \(S\) этого параллелограмма может быть вычислена по формулам: $$ S=\sqrt{\overline{a}^{\,2}\,\overline{b}^{\,2}-(\overline{a}\cdot\overline{b})^{2}}, \quad S=|x_1y_2-x_2y_1|. $$
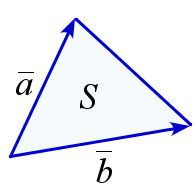
Площадь треугольника через скалярное произведение
Пусть векторы \(\overline{a}=(x_1,\, y_1)\), \(\overline{b}=(x_2,\, y_2)\) направлены вдоль сторон треугольника (координаты векторов – в ортонормированном базисе). Тогда площадь \(S\) этого треугольника может быть вычислена по формулам:
$$
S=\frac{1}{2}\sqrt{\overline{a}^{\,2}\,\overline{b}^{\,2}-(\overline{a}\cdot\overline{b})^{2}}, \quad
S=\frac{1}{2}|x_1y_2-x_2y_1|.
$$
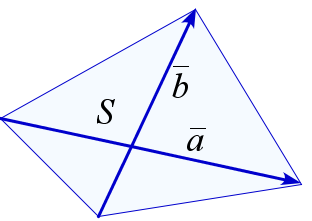
Площадь четырёхугольника через скалярное произведение
Пусть векторы \(\overline{a}=(x_1,\, y_1)\), \(\overline{b}=(x_2,\, y_2)\) направлены вдоль диагоналей четырёхугольника (координаты векторов – в ортонормированном базисе). Тогда площадь \(S\) этого четырёхугольника может быть вычислена по формулам: $$ S=\frac{1}{2}\sqrt{\overline{a}^{\,2}\,\overline{b}^{\,2}-(\overline{a}\cdot\overline{b})^{2}}, \quad S=\frac{1}{2}|x_1y_2-x_2y_1|. $$