Окружностью радиуса \(R>0\) с центром в точке \(O\) называется геометрическая фигура, состоящая из всех точек плоскости, которые находятся от точки \(O\) на расстоянии \(R\).

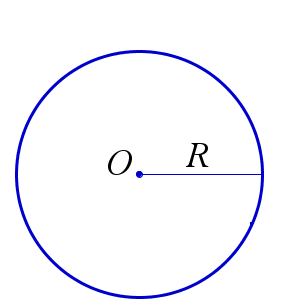
Окружность радиуса \(R\) с центром в точке \(O\)

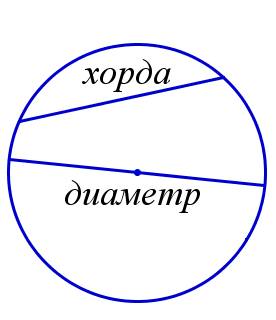
Отрезок с концами на окружности называется хордой окружности. Хорда, проходящая через центр окружности, называется диаметром окружности.

Отношение площадей подобных фигур равно квадрату коэффициента подобия.

$$ S_{\Phi_2}=k^2S_{\Phi_1} $$

Длина окружности радиуса \(R\) равна \(2\pi R\).

$$ l=2\pi R $$

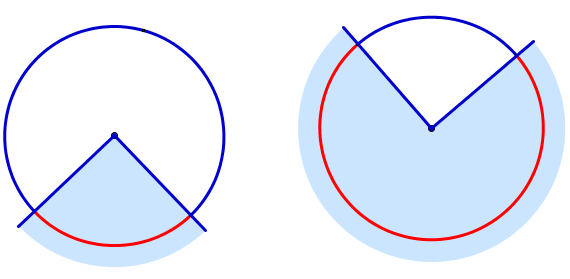
Дугой окружности называется геометрическая фигура, состоящая из всех точек окружности, принадлежащих некоторому плоскому углу с вершиной в центре этой окружности. Каждому такому углу соответствует ровно одна дуга окружности, и каждой дуге окружности соответствует ровно один плоский угол с вершиной в центре окружности.

Радианной мерой угла называется длина дуги окружности единичного радиуса с центром в вершине угла, которую этот угол высекает на окружности. Радианная мера развёрнутого угла равна \(\pi\), полного угла – \(2\pi\).

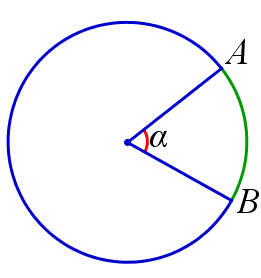
$$ \alpha=l_{\overset{\smile}{AB}} $$

Длина дуги окружности радиуса \(R\), соответствующей центральному углу радианной меры \(\alpha\), равна \(\alpha R\).

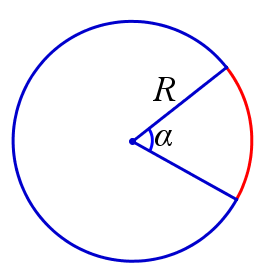
$$ l=\alpha R $$