Взаимное расположение двух окружностей
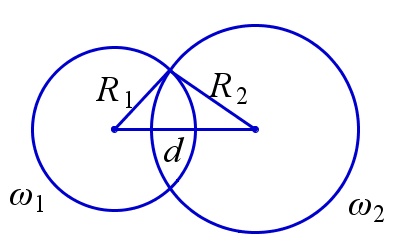
Пересекающиеся окружности
Говорят, что две окружности пересекаются, если они имеют две общие точки.
Пусть \(R_1\) и \(R_2\) – радиусы окружностей \(\omega_1\) и \(\omega_2\) и \(d\) – расстояние между их центрами. Окружности \(\omega_1\) и \(\omega_2\) пересекаются тогда и только тогда, когда числа \(R_1\), \(R_2\), \(d \) являются длинами сторон некоторого треугольника, т. е. удовлетворяют всем неравенствам треугольника: $$ R_1+R_2 > d, \, R_1+d > R_2, \, R_2+d > R_1. $$
Касающиеся окружности
Говорят, что две окружности касаются, если они имеют одну общую точку. Окружности касаются внутренним образом, если одна из них расположена внутри другой. Окружности касаются внешним образом, если они расположены вне друг друга.
Пусть \(R_1\) и \(R_2\) – радиусы окружностей \(\omega_1\) и \(\omega_2\) и \(d\) – расстояние между их центрами. Окружности \(\omega_1\) и \(\omega_2\) касаются внешним образом тогда и только тогда, когда \(R_1+R_2=d\), внутренним образом – когда \(\left|R_1-R_2\right|=d\).
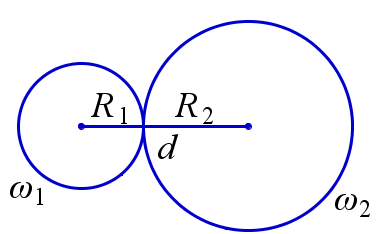 | 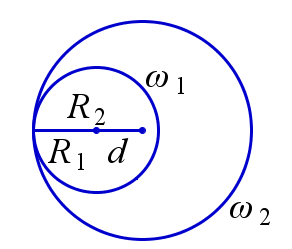 | ||
Внешнее касание | Внутреннее касание |
Непересекающиеся окружности
Говорят, что две окружности не пересекаются, если они не имеют общих точек. В этом случае одна из них лежит внутри другой, либо они лежат вне друг друга.
Пусть \(R_1\) и \(R_2\) – радиусы окружностей \(\omega_1\) и \(\omega_2\) и \(d\) – расстояние между их центрами. Окружность \(\omega_1\) и \(\omega_2\) расположены вне друг друга тогда и только тогда, когда \(R_1+R_2 < d\). Окружность \(\omega_1\) лежит внутри \(\omega_2\) тогда и только тогда, когда \(R_1+d < R_2\).
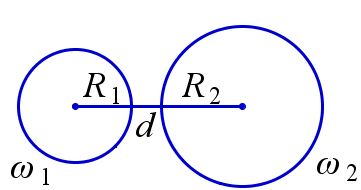 | 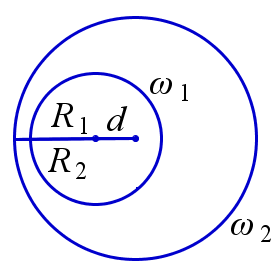 | ||
\(\omega_1\) и \(\omega_2\) вне друг друга | \(\omega_1\) лежит внутри \(\omega_2\) |