Непересекающиеся окружности

Говорят, что две окружности не пересекаются, если они не имеют общих точек. В этом случае одна из них лежит внутри другой, либо они лежат вне друг друга.

Пусть \(R_1\) и \(R_2\) – радиусы окружностей \(\omega_1\) и \(\omega_2\) и \(d\) – расстояние между их центрами. Окружность \(\omega_1\) и \(\omega_2\) расположены вне друг друга тогда и только тогда, когда \(R_1+R_2 < d\). Окружность \(\omega_1\) лежит внутри \(\omega_2\) тогда и только тогда, когда \(R_1+d < R_2\).

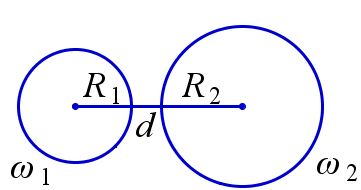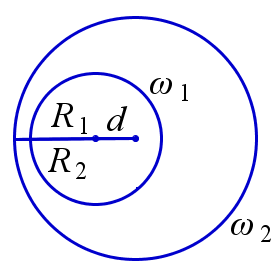\(\omega_1\) и \(\omega_2\) вне друг друга		\(\omega_1\) лежит внутри \(\omega_2\)