Касание и пересечение окружностей и прямых
❒ Взаимное расположение прямой и оружности
❒ Касательная и радиус окружности
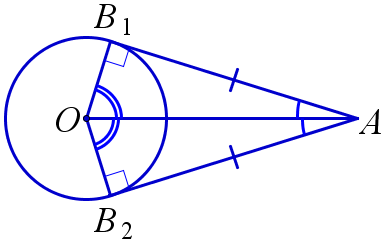
❒ Свойства касательных из одной точки к окружности
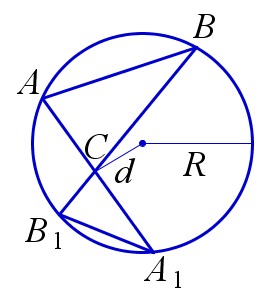
❒ Свойство хорд окружности
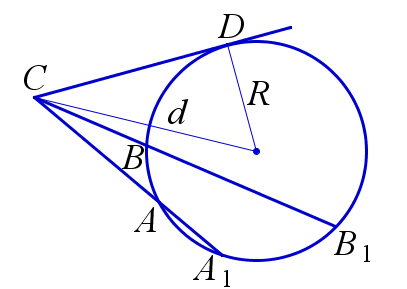
❒ Свойство секущих к окружности
Взаимное расположение прямой и оружности
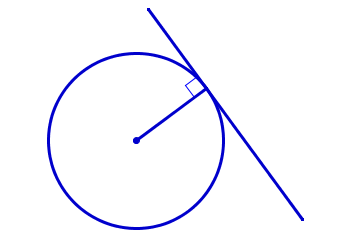
Говорят, что прямая и окружность пересекаются, если они имеют ровно две общие точки. В этом случае прямая называется секущей к окружности. Окружность и прямая касаются, если они имеют ровно одну общую точку. В этом случае прямая называется касательной к окружности, а общая точка прямой и окружности – их точкой касания. Прямая и окружность не пересекаются, если они не имеют общих точек.
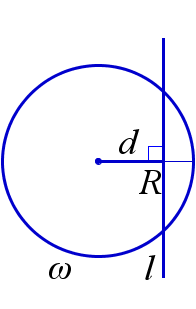
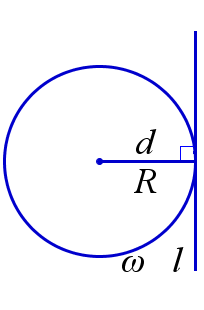
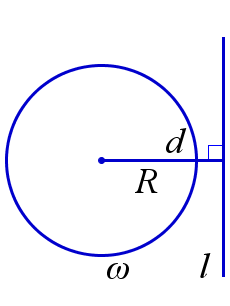
Пусть \(R\) – радиус окружности \(\omega\) и \(d\) – расстояние от центра окружности \(\omega\) до прямой \(l\). Тогда
\(\quad \quad \omega\) и \(l\) пересекаются \(\, \Leftrightarrow \, d < R\);
\(\quad \quad \omega\) и \(l\) касаются \(\, \Leftrightarrow \, d=R\);
\(\quad \quad \omega\) и \(l\) не пересекаются \(\, \Leftrightarrow \, d > R\).
 |
 |
 |
||
\(\omega\) и \(l\) пересекаются |
\(\omega\) и \(l\) касаются |
\(\omega\) и \(l\) не пересекаются |