Общее уравнение прямой на плоскости

Общим уравнением прямой в декартовой системе координат на плоскости называется уравнение вида \(Ax+By+C=0\), где \(A \neq 0\) или \(B \neq 0\).

Любое уравнение такого вида задаёт прямую, и любую прямую можно задать уравнением такого вида.

Если система координат прямоугольная, то вектор \(\overline{n} = (A,B)\) перпендикулярен данной прямой. Этот вектор называется нормальным вектором прямой.

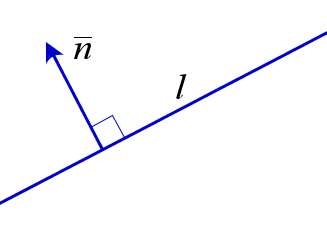$$ l: \quad Ax+By+C=0 $$ $$ \overline{n} = (A,B) $$