Прямоугольником называется четырёхугольник, все углы которого прямые.

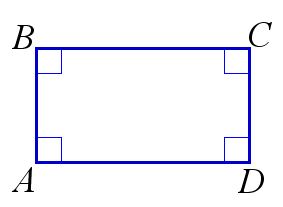
\(ABCD\) – прямоугольник

1. Прямоугольник является параллелограммом.
2. Диагонали прямоугольника равны.
3. Около прямоугольника можно описать окружность. Центром этой окружности является точка пересечения диагоналей прямоугольника.

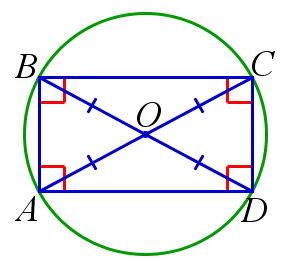
\(ABCD\) – прямоугольник \(\, \Rightarrow \, \) \(ABCD\) – параллелограмм;
\(ABCD\) – прямоугольник \(\, \Rightarrow \, \) \(AC=BD\);
\(ABCD\) – прямоугольник \(\, \Rightarrow \, \) \(ABCD\) вписанный

1. Если четырёхугольник является параллелограммом и один из его углов прямой, то этот четырёхугольник – прямоугольник.
2. Если четырёхугоьник является параллелограммом и его диагонали равны, то этот четырёхугольник – прямоугольник.
3. Если четырёхугоьник является параллелограммом и его можно вписать в окружность, то этот четырёхугольник – прямоугольник.

Площадь прямоугольника равна произведению его смежных сторон.

$$ S=ab $$