Ромб – это четырёхугольник, все стороны которого равны между собой.

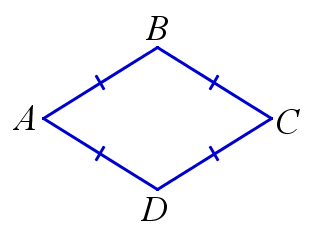
\( ABCD\) – ромб

1. Ромб является параллелограммом.
2. Диагонали ромба перпендикулярны.
3. Диагонали ромба лежат на биссектрисах его углов.
4. В ромб можно вписать окружность. Центром этой окружности является точка пересечения диагоналей ромба.

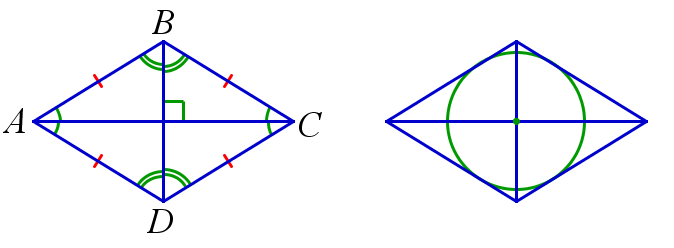
\(ABCD\) – ромб \(\Rightarrow\) \(ABCD\) – параллелограмм\(;\)
\(ABCD\) – ромб \(\Rightarrow\) \( AC \perp BD; \)
\(ABCD\) – ромб \(\Rightarrow\) \(\angle{BAC}=\angle{DAC}=\angle{BCA}=\angle{DCA}, \) \( \angle{ABD}=\angle{CBD}=\angle{ADB}=\angle{CDB}\)

1. Если диагонали четырёхугольника перпендикулярны и делятся точкой пересечения пополам, то этот четырёхугольник – ромб.
2. Если диагонали четырёхугольника лежат на биссектрисах его углов, то этот четырёхугольник – ромб.
3. Если четырёхуголльник параллелограмм и в него можно вписать окружность, то этот четырёхугольник – ромб.

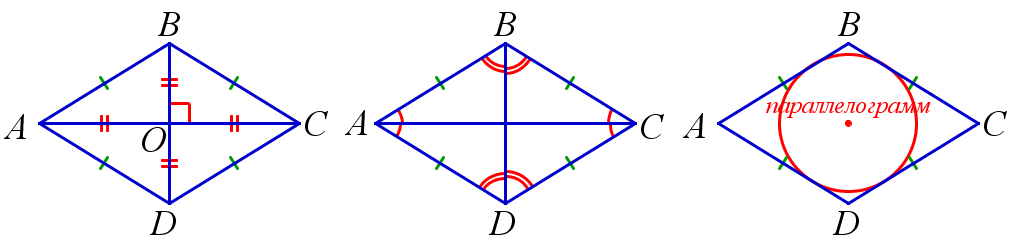
\( AC \perp BD, \, AO=CO, \, BO=DO \) \(\Rightarrow\) \(ABCD\) – ромб\(;\)
\( \left. \begin{matrix} \angle{BAC}=\angle{DAC}, \, \angle{BCA}=\angle{DCA} \\ \angle{ABD}=\angle{CBD}, \, \angle{ADB}=\angle{CDB} \\ \end{matrix} \right\} \Rightarrow\) \( \, ABCD\) – ромб;
\( AB||CD, \, BC||AD,\, ABCD\) – описанный \( \, \Rightarrow \, \) \( \, ABCD\) – ромб

Площадь ромба равна половине произведения его диагоналей.