Площадь круга радиуса \(R\) равна \(\pi R^2\).

$$ S=\pi R^2 $$

Площадь кругового сектора равна \(\frac{1}{2}\alpha R^2\), где \(\alpha\) – радианная мера центрального угла, отвечающего данному сектору, \(R\) – радиус круга.

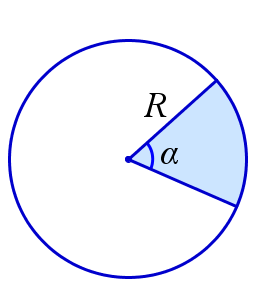
$$ S=\frac{1}{2}\alpha R^2\ $$

Площадь кругового сегмента равна \(\frac{1}{2}(\alpha - \sin{\alpha})R^2\), где \(\alpha\) – радианная мера центрального угла, отвечающего данному сегменту, \(R\) – радиус круга.

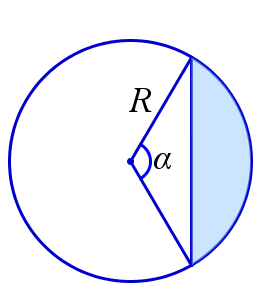
$$ S=\frac{1}{2}(\alpha - \sin{\alpha}) R^2\ $$