Каноническое уравнение прямой, проходящей через данную точку с заданным направляющим вектором

В декартовой системе координат уравнение прямой \(l\), проходящей через точку \(M_0(x_0, y_0)\) параллельно ненулевому вектору \(\overline{a}=(a_1,a_2)\) имеет вид

$$ \dfrac{x-x_0}{a_1}=\dfrac{y-y_0}{a_2}. $$

Другая форма: \(a_2(x-x_0)-a_1(y-y_0)=0.\)

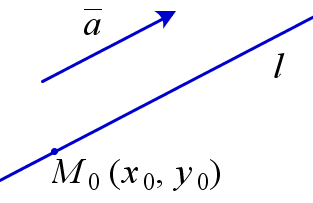
Ненулевой вектор, параллельный данной прямой или лежащий на ней, называется направляющим вектором этой прямой.