Уравнение прямой с угловым коэффициентом

Уравнение вида \(y=kx+b\) задаёт в прямоугольной декартовой системе координат прямую \(l\), не параллельную оси ординат. Число \(k\) называется угловым коэффициентом прямой \(l\). Угловой коэффициент прямой равен тангенсу угла наклона прямой \(l\) к положительному направлению оси абсцисс. Угол наклона отсчитывают от этой оси до прямой \(l\) против часовой стрелки. Если прямая \(l\) параллельна оси абсцисс или совпадает с нею, то угол наклона считается нулевым.

Коэффициент \(b\) равен ординате точки пересечения прямой \(l\) с осью ординат.

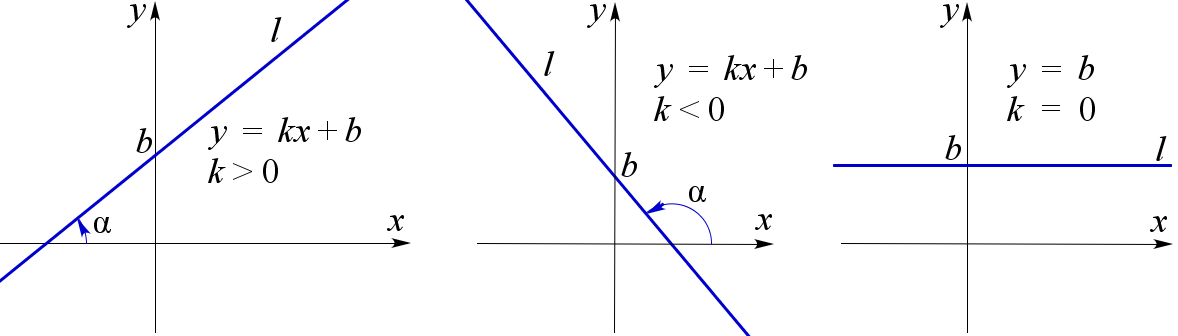
$$ k=\tg{\alpha} $$