Сложение векторов
❒ Сумма векторов
❒ Правило параллелограмма
❒ Нулевой вектор
❒ Противоположный вектор
❒ Свойства сложения векторов
❒ Разность векторов
Сумма векторов
Векторы можно складывать между собой, и при этом сумма векторов также является вектором. Основное свойство сложения векторов называется правилом треугольника.
Правило треугольника
$$ \overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC} $$
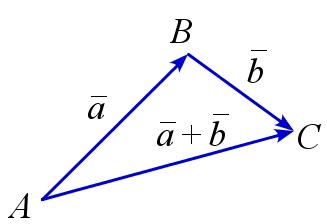
Правило параллелограмма
Если \(ABDC\) – параллелограмм, то \(\overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{AD}\).

$$ \overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{AD} $$
Нулевой вектор
Вектор, задаваемый направленным отрезком, начало и конец которого совпадают, называется нулевым вектором. Нулевой вектор обозначается \(\overline{0}\). Таким образом, \(\overrightarrow{AA}=\overline{0}\) для любой точки \(A\). И обратно, если \(\overrightarrow{AB}=\overline{0}\), то точки \(A\) и \(B\) совпадают.
Противоположный вектор
Вектор \(-\overline{a}=\overrightarrow{BA}\) называется противоположным вектору \(\overline{a}=\overrightarrow{AB}\). Если \(B'\) – точка, симметричная \(B\) относительно точки \(A\), то справедливо равенство \(\overrightarrow{AB'}=-\overrightarrow{AB}\).
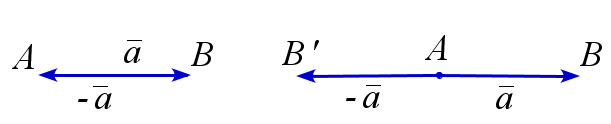
Свойства сложения векторов
1. \(\overline{a}+\overline{b}=\overline{b}+\overline{a}\) для любых векторов \(\overline{a}\) и \(\overline{b}\);
2. \(\left( \overline{a}+\overline{b} \right) + \overline{c}=\overline{a}+ \left(\overline{b}+\overline{c} \right)\) для любых векторов \(\overline{a}\), \(\overline{b}\) и \(\overline{c}\);
3. \( \overline{a} + \overline{0} = \overline{0} + \overline{a} = \overline{a}\) для любого вектора \(\overline{a}\);
4. \( \overline{a} +(-\overline{a}) = (-\overline{a}) + \overline{a} = \overline{0}\) для любого вектора \(\overline{a}\).
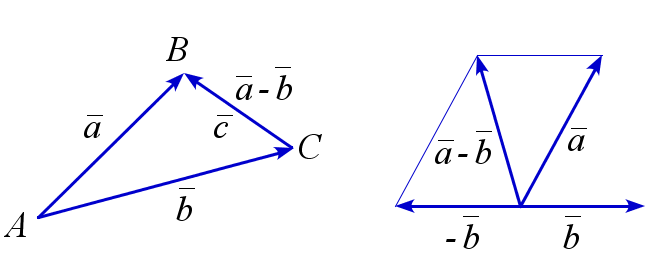
Разность векторов
Разностью векторов \(\overline{a}\) и \(\overline{b}\) называется такой вектор \(\overline{c}\), что \( \overline{a}=\overline{b} + \overline{c}\). Из правила треугольника следует, что \(\overrightarrow{AB}-\overrightarrow{AC}=\overrightarrow{CB}\). Кроме того, справедливо равенство \(\overline{a}-\overline{b}=\overline{a}+(-\overline{b})\).