Произведением вектора \(\overline{a}=\overrightarrow{AB}\) на действительное число \(\lambda\) называется вектор \(\lambda\overline{a}=\overrightarrow{AC}\), удовлетворяющий следующим условиям:
   1. \(A\), \(B\) и \(C\) лежат на одной прямой;
   2. \(AC=|\lambda|\,AB\);
   3. если \(A \neq B\), то при \(\lambda>0\) \(B\) и \(C\) лежат по одну сторону от \(A\), при \(\lambda<0\) \(B\) и \(C\) лежат по разные стороны от \(A\).

Для любых векторов \(\overline{a}\) и \(\overline{b}\) и любых чисел \(\lambda\) и \(\mu\) справедливы равенства:
   1. \(\lambda(\mu\overline{a})=(\lambda\mu)\overline{a}\);
   2. \((\lambda\pm\mu)\overline{a}=\lambda\overline{a}\pm\mu\overline{a}\);
   3. \(\lambda(\overline{a}\pm\overline{b})=\lambda\overline{a}\pm\lambda\overline{b}\);
   4. \(1\overline{a}=\overline{a}\);
   5. \(0\overline{a}=\overline{0}\);
   6. \((-1)\overline{a}=-\overline{a}\);
   7. \(\lambda\overline{a}=\overline{0} \, \Leftrightarrow \, \lambda=0\) или \(\overline{a}=\overline{0}\).

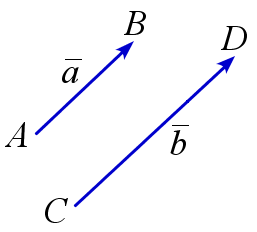
Векторы \(\overline{a}\) и \(\overline{b}\) называются коллинеарными (обозначение: \(\overline{a}|| \overline{b}\)), если существует число \(\lambda\) такое, что \(\overline{a}=\lambda\overline{b}\) или \(\overline{b}=\lambda\overline{a}\). Векторы \(\overrightarrow{AB}\) и \(\overrightarrow{CD}\) коллинеарны тогда и только тогда, когда хотя бы один из них нулевой, либо прямые \(AB\) и \(CD\) параллельны или совпадают.

\(\overline{a}\) и \(\overline{b}\) коллинеарны		\(\overline{a}\) и \(\overline{b}\) не коллинеарны

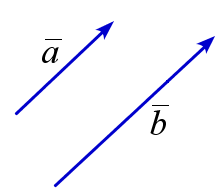
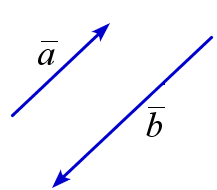
Ненулевые коллинеарные векторы \(\overline{a}\) и \(\overline{b}\) называются одинаково направлнными (обозначение: \(\overline{a}\upuparrows \overline{b}\)), если существует число \(\lambda>0\) такое, что \(\overline{a}=\lambda\overline{b}\), и противоположно направленными (обозначение: \(\overline{a}\uparrow\downarrow \overline{b}\)), если существует \(\lambda<0\) такое, что \(\overline{a}=\lambda\overline{b}\).

\(\overline{a}\) и \(\overline{b}\) одинаково направлены		\(\overline{a}\) и \(\overline{b}\) противоположно направлены