Разложение вектора по базису
Понятие базиса
Базисом векторов на плоскости называется пара ненулевых неколлинеарных векторов \(\overline{e}_1\), \(\overline{e}_2\).
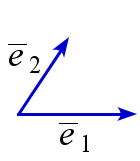
Разложение вектора по базису
Пусть \(\overline{e}_1\), \(\overline{e}_2\) – базис векторов на плоскости. Тогда любой вектор \(\overline{a}\) можно разложить по этому базису, то есть представить в виде \(\overline{a}=x\overline{e}_1+y\overline{e}_2\). Числа \(x\) и \(y\) определены при этом однозначно и называются координатами вектора \(\overline{a}\) в базисе \(\overline{e}_1\), \(\overline{e}_2\). При фиксированном базисе пишут: \(\overline{a}=(x,\,y)\).
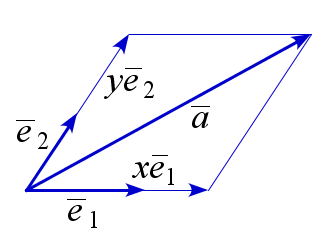
$$ \overline{a}=x\overline{e}_1+y\overline{e}_2 $$
Операции над векторами в координатах
Пусть \(\overline{a}=(x_1,\,y_1)\) и \(\overline{b}=(x_2,\,y_2)\) – координаты векторов \(\overline{a}\) и \(\overline{b}\) в одном и том же базисе. Тогда координаты векторов \(\overline{a}\pm\overline{b}\) и \(\lambda\overline{a}\) (\(\lambda\in\mathbf{R}\)) могут быть вычислены по формулам:
$$
\overline{a}\pm\overline{b}=(x_1\pm x_2,\,y_1\pm y_2); \quad
\lambda\overline{a}=(\lambda x_1,\,\lambda y_1).
$$