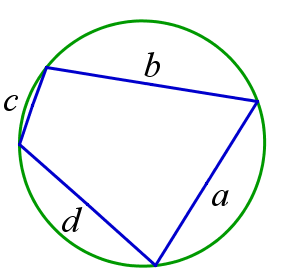
Вписанный четырёхугольник
❒ Определение вписанного четырёхугольника
❒ Центр описанной окружности вписанного четырёхугольника
❒ Критерий вписанного четырёхугольника
❒ Площадь вписанного четырёхугольника
Определение вписанного четырёхугольника
Четырёхугольник называется вписанным, если все его вершины лежат на некоторой окружности.
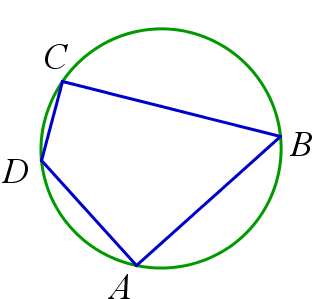
\(ABCD\) – вписанный четырёхугольник
Центр описанной окружности вписанного четырёхугольника
Четырёхугольник можно вписать в окружность тогда и только тогда, когда серединные перпендикуляры к его сторонам пересекаются в одной точке. Центром описанной окружности вписанного четырёхугольника является точка пересечения серединных перпендикуляров к его сторонам.
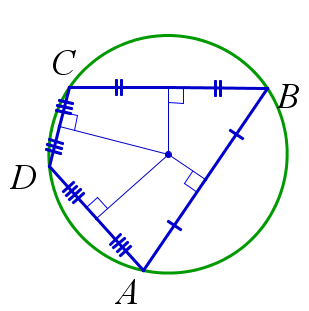
Критерий вписанного четырёхугольника
Четырёхугольник можно вписать в окружность тогда и только тогда, когда сумма его противоположных углов равна \(180^{\circ}\).
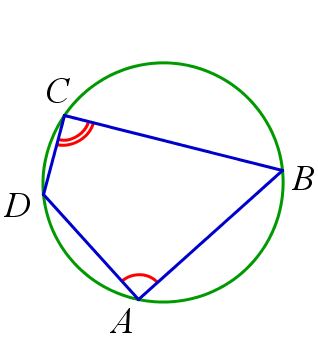
\(ABCD\) – вписанный \(\, \Leftrightarrow \, \angle{A}+\angle{C}=180^{\circ} \)
Площадь вписанного четырёхугольника
Площадь вписанного четырёхугольника может быть вычислена по формуле $$ S=\sqrt{(p-a)(p-b)(p-c)(p-d)}, $$ где \(a\), \(b\), \(c\), \(d\) – длины сторон четырёхугольника, \(p=\frac{1}{2}(a+b+c+d)\) – его полупериметр.